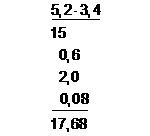Brøk ganget med brøk

Hva betyr det å gange to brøker med hverandre? Hva er det man gjør når man tar ?

Det er alltid spennende å spørre skoleelever, studenter eller andre om dette, for det råder mye forvirring om svaret. Blir det en kvart eller blir det en hel? Når det er så mye usikkerhet om dette, skyldes det selvfølgelig at folk ikke har noen klar formening om hva som egentlig foregår. Dette ser man tydelig hvis man ber elevene lage en tekst som passer til oppgaven. Man kan få de underligste svar[1], mens fornuftige svar gjerne glimrer med sitt fravær. Poenget er at vi må tolke denne oppstillingen på samme måte som over. Vi skal finne halvparten av en halv, slik at . For ordens skyld: hvis vi skal finne halvparten av en tredel, bør vi etter vår logikk skrive det som .

Legg for øvrig merke til at svarene blir ganske opplagte når man først klarer å finne logikken bak multiplikasjonen. Det er også veldig enkelt å finne praktiske situasjoner på multiplikasjon av brøk med brøk.

            Når man først har satt seg inn i tankegangen, er det også enkelt å utvide perspektivet til å lage oppstillinger som omfatter mer enn én opplysning. La meg ta et par eksempler.

Din gamle tante dør og du skal være med å dele arven på 1 200 000 kr. Arven skal deles likt mellom hennes tre søsken. Men den ene søsteren, din mor, er allerede borte, så du og dine tre søsken skal dele din mors andel.

Du får:

Du skal beregne rente av 15 000 kr i 120 dager til rentefot 3 % p.a.

Renter:

I den siste eksempelet har brukt den tradisjonelle oppstillingen. Dersom vi skulle vært konsekvente, burde vi skrevet

. Dette er imidlertid et såpass stort brudd på det som vanligvis brukes, at jeg ikke uten videre vil anbefale å gjøre det. Det er viktigere å vise at begge oppstillingsmåtene kan brukes, og så la elevene velge selv. En slik holdning vil være i tråd med den generelle metodikken jeg forsøker å formidle.

En annen sak er at mange elever har vansker med å forstå at man kan skrive inn flere tanketrinn i én felles oppstilling. De skiller ikke mellom antall regneoperasjoner og oppstillingene. Dette problemet henger sammen med den ulykksalige metodikken med først å gjøre utregninger, for så å avslutte med en såkalt svarsetning, i stedet for å bruke tekster, oppstillinger og resultat overalt. Å kunne skrive inn flere tanketrinn i en felles oppstilling, slik som over, har stor overføringsverdi til mange former for prosentregning, slik som rentesrente eller beregning av flere års prosentvise endringer (f.eks. konsumprisindeks), og mye annet.

 

Regneteknikk

Hovedregelen for å regne ut produktet av to brøker er å gange to brøker med hverandre er å gange teller med teller og nevner med nevner. Hvis vi følger denne, får vi raskt og automatisk at . Ofte er det imidlertid lurest  å forkorte først. Hvis vi for eksempel skal finne ut hvor mye to tredeler av ni fjortendeler er, vil vi få oppsettet. Her lønner det seg å forkorte før man utfører noen multiplikasjon:

Her er 2 og 14 delt med 2, mens 9 og 3 er delt med 3. Legg merke til at det ikke er noe i veien for å forkorte tall i ulike brøker mot hverandre. Dette kommer av at ifølge hovedregelen for å gange brøker.

            Å kunne forkorte er alltid nyttig. La meg ta noen eksempler.

           

Den siste brøken er oppsettet du får om du skal regne ut hvor mange ulike rekker man kan lage i Lotto. Her kan man få problemer hvis man bruker kalkulator og prøver å regne rett ut, for en vanlig kalkulator har ikke kapasitet til å regne ut telleren nøyaktig, og hvis man vekselvis deler og ganger, vil man få unødvendige og unøyaktige desimaltall.

Mange elever har for øvrig problemer med å slå inn brøker korrekt på kalkulator. Hvis man skal regne ut , slår de gjerne inn 30 000 - delt på 365 - ganget med 12, i

stedet for å dele også med 12. De har problemer med å forstå at tallet i telleren skal deles med hvert av tallene i nevneren, eller med produktet av dem selvfølgelig, men da må man sette parentes rundt faktorene i nevneren, hvis dette er mulig på den kalkulatoren som er i bruk. Hvis ikke må man finne mellomsvaret (trykke på likhetstegnet) og dele på nytt.

---

[1] Én variant var følgende: ”En gutt skulle dele en halv sjokolade med halvbroren sin”

Multiplikasjon av helt tall med brøk

Dersom man har innført likeverdige brøker slik som omtalt over, har man fått med seg multiplikasjon av brøk med helt tall gratis. Temaet er både konkretisert og avmystifisert på en gang. En gang i min tid som matematikklærer i ungdomsskolen ga jeg elevene i 10. klasse ei prøve med repetisjonsstoff. På slutten av prøva ba jeg elevene skrive ned noen tanker om hvilke oppgaver de syntes var lette og hvilke de syntes var vanskelige. Prøva inneholdt etter min vurdering en god del krevende oppgaver. Det var derfor svært overraskende at den desidert flinkeste eleven i klassa svarte at den eneste oppgaven han hadde hatt problemer med var å finne av 24! Dette var en elev som fikk beste karakter på samtlige matematikkprøver gjennom hele ungdomsskolen, noe som er meget uvanlig. Denne hendelsen har fulgt meg siden, for det var en skikkelig vekker med hensyn til den måten vi bedriver opplæring i brøkregning i skolen. Egentlig er det nesten utrolig at en så flink elev skulle ha problemer med et slikt filleproblem. Det viser imidlertid nødvendigheten av å være mer bevisst på hvordan vi håndterer dette stoffet.

            Hvis vi skal regne ut for eksempel av 24, og lage en formell oppstilling, hvordan skal vi føre det? Det riktigste logisk sett er å skrive . Dette er i tråd med den måten vi leser oppstillingen. Ordet av blir her oversatt til multiplikasjonstegn, akkurat som ordet og blir oversatt til addisjonstegn. Denne oversettelsen er fruktbar i forbindelse med multiplikasjon med brøk. Vi kan jo også bruke ordet av hvis vi skal forklare multiplikasjoner med hele tall, selv om det er et kunstgrep. Etter dagens norske standard står multiplikator foran multiplikand. Dette betyr at . Vi har tre forekomster av tallet 4. I brøkeksempelet vårt har vi fem seksdeler av tallet tjuefire. Slik sett tar vi med denne skrivemåten vare på den logikken som brukes ellers i multiplikasjon, selv om det virker litt kunstig.

            Hvilken logikk får vi så hvis vi bytter om rekkefølgen? Dersom vi følger tankegangen om at et produkt av to faktorer skrives i rekkefølge multiplikator ganget med multiplikand, får vi da den enkle sammenhengen at (24 ganger). Dette er jo greit, og kan godt brukes som utgangspunkt for å forklare hva som skjer når man ganger en brøk med et helt tall, men da vil man gå glipp av sammenhengen med momentet over, å finne en viss brøkdel av et tall.

Jeg synes uansett ikke det er noe i veien for å bytte rekkefølgen. Multiplikasjon med tall må uansett utvides til å gjelde situasjoner der begrepene multiplikator og multiplikand mister sin betydning. Hvis du skal finne hvor mye du må betale for strømforbruket ditt, må du for eksempel regne ut . Her er det ikke særlig hensiktsmessig å tenke i multiplikand og multiplikator. Dessuten er det viktig at elevene vender seg til at multiplikasjon er kommutativ (så lenge vi ikke jobber med mer avansert matematikk som vektorer eller grupper).

            I min skoletid het skolefaget regning, ikke matematikk. I praktiske oppgaver skrev vi av 24 som (med benevning). I tråd med logikken over, kunne vi i dag skrive .

Fordelen med dette er at det lett kan brukes til å angi en nyttig måte å tenke på, nemlig det vi kaller veien om én. Vi finner da først av 24 ved å dele 24 med 6. Deretter ganger vi med 5 og får 20. Denne tenkemåten har dessverre langt på vei blitt borte i skolen. Dette er dumt, for den har stor verdi i blant annet prosentregning. Samtidig viser den at det lønner seg å dele før du ganger, dersom divisjonen går opp.

            Altfor ofte, ja nesten uten unntak, kan vi se yngre mennesker regne slik: , eller enda verre:

. Når folk regner slik, får vi en overtydelig demonstrasjon av at brøkregningen har blitt et ritual, og at den er dårlig fundert i praktiske erfaringer. At det tredobbelte av en tredel er en hel, burde være en selvfølge som ikke krever noen som helst slags mellomregning. Hvis vi har tre tredels liter saft, så må jo dette være en hel liter! I det første tilfellet bør vi, slik som omtalt over, starte med å dele seks med tre, for så å ta det dobbelte. Her riktignok tallene så enkle at vi like gjerne kan gange først, men det kan i alle fall være greit å ha den første metoden for øye når tallene gjør utregningen enklere. Dette med å gjøre om hele tall til uekte brøk med nevner 1, kan nok være et praktisk knep når man jobber med algebra, men egentlig er det helt unødvendig.

    

Linjer videre

Når man kommer så langt at praktiske oppgaver blir innviklede, kan det være nyttig å ta i bruk ligning som løsningsmetode. Ofte ser vi elever og studenter ikke mestrer å sette opp enkle ligninger når det er brøk med i bildet. La meg ta et par eksempler:

Eksempel 1:

Ei flaske brus uten pant koster 12 kr. Panten utgjør 1/5 av pris med pant. Hvor mye koster flaska med pant?

Dersom vi bruker ligning, blir løsningen slik:

Flaska koster x kr.

Flaska koster 15 kr.

Å regne dette kan by på problemer. Først må du tenke ut at prisen uten pant utgjør 4/5 av prisen med pant. Så kan du si at 1/5 av prisen er lik 3 kroner, og da er prisen med pant lik 15 kr. Mange elever forsøker imidlertid å løse dette praktisk, med eller uten hell, selv om de vet at de med fordel kan bruke ligning. Hovedårsaken til at de ikke bruker ligning, er som oftest at de ikke klarer å sette opp første ledd i ligninga, dvs. at panten skal settes lik 1/5 av x, dvs. . De har en sterk tilbøyelighet til å sløyfe x-en. De har ikke tilstrekkelig innsikt i hva det vil si å gange et helt tall med en brøk.

Eksempel 2. Dette er lite grann mer innviklet og lyder slik:

På en fisk veier hodet 1/3 av fiskens vekt, halen veier 1/4, mens resten av kroppen veier 300 gram. Hvor mye veier fisken.

Jeg har sett løsninger på dette som er både forseggjorte og riktige, men hvor man har gått over bekken etter vann flere ganger. Også de løsningene har bunnet seg i at studentene ikke har maktet å sette opp ligningen. Typisk er det å skrive at . Dette klarer man ikke å oversette til ligning, slik som følger:

Fisken veier x gram.

Fisken veier 720 gram

Nok en gang er problemet å få med x-en i de første leddene. Og nok en gang må lærdommen være at man må arbeide med sammenhenger og forståelse.

     

Å finne en viss brøkdel av et tall. Likeverdige brøker

Ofte blir utviding og forkorting av brøker framstilt på en nokså abstrakt måte. Man bruker gjerne tallinje eller tilsvarende ting for å vise at brøkene beholder samme verdi når de utvides eller forkortes. Før dette kan også selve brøkbegrepet ha blitt introdusert på en abstrakt måte, som et uttrykk som består av en teller og en nevner. Det rituelle aspektet ved brøkregningen er der da fra første stund av! Hvorfor ikke starte med å finne en viss brøkdel av noe som elevene kjenner til, for eksempel å finne hvor mange elever  av ei klasse på 21 elever, eller tilsvarende, er. Så kan man undersøke om , … av klassa blir like mye. Ideelt sett bør dette skje gjennom en problemløsningssekvens, men det avgjørende er at elevene får være med å tenke gjennom problemet og å finne hensiktsmessige illustrasjoner (representasjoner). På denne måten vil man få en naturlig innsikt i at brøkene over er likeverdige. Tilsvarende kan man selvfølgelig gjøre med forkorting av brøk, ved at man starter med en brøk som kan forkortes på en eller flere måter. Man bør ikke starte med den formelle teknikken med å multiplisere og dividere teller og nevner med samme tall. Det bør være en ”oppdagelse” man gjør underveis.

            Det endelige målet er, her som ellers, at den innledende sekvensen blir en prototyp for videre regning og abstrahering. Men her kan det som sagt lønne seg å ta seg god tid. Mange elever vil ha behov for å gå tilbake til praktiske situasjoner mange ganger. Dessuten bør man jobbe med målte verdier, ikke bare antall. Elevene er ganske sikkert fortrolige med begreper som liter eller meter, og kanskje kilogram. Da bør man også finne brøkdeler av størrelser som er målt, som for eksempel å finne ,… av en veistrekning på 800 meter. Mulighetene til å finne praktiske eksempler er uuttømmelige.

BRØKREGNING (Vil bli delt i mange mindre deler - er svært omfattende)

Hva er en brøk?

Brøker brukes som bekjent for å betegne en mengde som ikke er hel. Vi kan snakke om en halv sjokolade eller en kvart liter brus, og opprinnelig er det ganske sikkert eksempler som er analoge til dette, som ble brukt i hulen, over leirbålet eller på jakt. Nøyaktigere bruk av brøk og regning med brøk kom sikkert ikke før ei god stund etter jordbruksrevolusjonen. Vi vet imidlertid at brøkregning ble brukt i de gamle jordbrukskulturene. De gamle egypterne brukte merkelig nok bare stambrøker, dvs. brøker med teller lik 1, med unntak av , men til gjengjeld var de svært dyktige til å regne med disse[1].

            Viktigst i vår sammenheng er det at brøker kan betraktes på samme måte som hele tall, dvs. at man kan bruke dem som konkrete enheter eller som abstrakte tall, som ”adjektiv” eller som ”pronomen”. Vi kan snakke om halv kilometer eller om det abstrakte tallet . Målet i skolen må være å få elevene til å beherske regning med de abstrakte tallene, akkurat slik som målet for regning med de hele tallene er. Brøkregning er imidlertid mye mer innviklet enn regning med hele tall, og barnas erfaringer med brøk er langt færre enn med bruk av hele tall[2]. Derfor er det nødvendig å beholde tilknytningen til praktisk erfaring mye lengre enn når det gjelder de hele tallene. Mer formelle definisjoner av brøk er ikke nødvendige i grunnskolen, men det kan være formålstjenlig å snakke om brøk som det inverse av hele tall. Begrepet invers kan i det hele tatt være nyttig, da det brukes mye både i ren matematikk og anvendelser innen naturvitenskap.

Når det gjelder abstrahering begår vi sannsynligvis en dobbelt synd i grunnskolen, ved at vi er for lite flinke til å abstrahere regning med hele tall, mens vi abstraherer brøkregning for tidlig, eller ved at vi reduserer all brøkregning til et ritual uten konkret tilknytning. For mange elever er det sannsynligvis nødvendig å støtte seg til halvabstrakter i brøkregningen helt ut ungdomsskolen. Det er så mange ulike situasjoner (prototyper) å holde styr på, at vi må ha noe å støtte oss til. Men det er likevel viktig å holde klart for seg, at jo flinkere vi er til å finne gode prototyper, og jo bedre vi er til å vise elevene sammenhenger, jo lettere blir det for dem å abstrahere brøkregningen.

I hvilken rekkefølge bør brøkregning undervises?

Den tradisjonelle rekkefølgen er å starte med addisjon og subtraksjon, etter at definisjoner og likeverdige brøker, dvs. utvidelse og forkorting, er gjennomgått. Multiplikasjon og divisjon har vært ansett som vanskeligere og har derfor blitt tatt til sist. Selv mener jeg dette er feilaktig, og i den videre teksten håper jeg å godtgjøre at det er lettere å finne praktiske og enkelt forståelige eksempler på multiplikasjon og divisjon med brøk, enn det er å finne for addisjon og subtraksjon. Slik sett burde man snu den tradisjonelle rekkefølgen. Dersom man legger vekt på problembasert undervisning, blir imidlertid dette spørsmålet mindre interessant, for da er det naturlig å introdusere alle regningsarter tidlig i prosessen. Også dette er i tråd med hva som i dag anbefales for regning med hele tall.

---

[1] Det sies at i det tidligere tsar-Russland ble det brukt bare brøker av typen , noe som kunne føre til betydelige unøyaktigheter ved beregning av store landeiendommer.

[2] Brøk brukes for øvrig mer i engelskspråklige land der man fortsatt bruker mile og tommer som lengdemål.

Desimaltall

Forstavelsen desi er en forkortelse av det latinske ordet decimus, som betyr den tiende (nummer ti I rekken). Ordet desimaltall er derfor egentlig en betegnelse for titallssystemet, og slik brukes det også på engelsk. Det vi kaller desimaltall, kalles der for decimal fractions, desimalbrøker, som kan oversettes til tidelsbrøker. Før var det vanlig å bruke denne betegnelsen (desimalbrøk) også på norsk, men dette synes å ha blitt helt borte. På en måte er det synd, for denne betegnelsen forteller mer om hva desimaltall er enn hva ordet desimaltall gjør.

            Titallssystemet har en lang historie, sannsynligvis fra oldtidens Kina, via India og til middelalderens arabere. Den kjente matematikeren (Abu Ja'far Muhammad ibn Musa) Al-Khwarizmi[1], ca. 780 – 840 e.Kr., arbeidet i Kunnskapens hus i Bagdad. Han introduserte de indiske tallene, dvs. titallssystemet og tallet 0. Leonardo de Pisa, senere kalt Fibonacci (sønn av Nacci) førte tallene til Europa gjennom sin kjente bok Liber Abacci, Kunsten å regne, utgitt i 1202 e.Kr.

Den første som utvidet tallsystemet til å gjelde tidelsbrøker ( osv.), var (Abu'l Hasan Ahmad ibn Ibrahim) Al-Uqlidisi (ca. 920 - 980). Det ser imidlertid ikke ut til at hans system ble tatt i bruk i særlig grad. Den som innførte desimalbrøkene slik at systemet slo gjennom for godt, var belgieren Simon Stevin (1548—1620). Desimalkommaet kom imidlertid senere, så Stevin brukte en notasjon som I dag synes tungvint. Det synes å være litt uklart om det var den tyske munken Christopher Clavius[2] (1538 – 1612) eller skotten John Napier[3] (1550 – 1617) som først innførte dette.

Stevin skrev desimaltall på følgende måte: 6i4j2k5l6m (= 6,4256). Han kalte desimalbrøkene for henholdsvis ”de første”, ”de andre” osv. Verdiene forklarer han slik: De nevnte tallene er 6 hele, 4/10, 2/100, 5/1000 og 6/10000, til sammen 64256/10000. Han legger til at ”unntatt for i, overskrider aldri et siffer verdien 9; for eksempel ikke 7j12k, men 8j2k”.

Sammenhenger i tallsystemet

Selv om man demper ned vektleggingen av posisjonenes betydning i den første innlæringen av tallsystemet, er det viktig at barna får tak i de grunnleggende sammenhengene i systemet. Ikke minst er dette sentralt for forståelsen av desimaltallene. Om man legger vekt på mengder eller på den mer formelle strukturen, er det viktig å få fram at det er ti enere i ti, ti tiere i hundre, ti hundrer i tusen og så videre oppover. I desimalene er det ti tideler i en ener, ti hundredeler i en tidel, ti tusendeler i en hundredel osv. Vi kan altså skrive at 0,1 = 0,10 = 0,100, eller at . Dette betyr at for eksempel tallet 7,453 kan uttrykkes som ”sju hele, 4

tideler, 5 hundredeler og 3 tusendeler”, men også som ”sju hele og 453 tusendeler”, eller for den saks skyld ”sju hele, 45 hundredeler og 3 tusendeler. Skrevet med brøk blir det slik: .

            Slike sammenhenger er av avgjørende betydning for å forstå ulike måleenheter. I vår tid er de fleste måleenhetene som er i bruk, bygd opp omkring titallsystemet. Elever i grunnskolen bør vite at 1 km = 1000 m, at 1 kg = 10 hg = 1000 g, og gjerne at 1 dekar = 10 ar = 1000 m². De bør også forstå at 1 m = 10 dm = 100 cm = 1000 mm, og derfor er 1 dm = 10 cm = 100 mm, og 1 cm = 10 mm.

            En enkel metode for å synliggjøre slike sammenhenger, kan være å bruke følgende tabell:

 

 

Her er det er en faktor på 10 mellom hver linje i tabellen. Tallet 0,6 er ti ganger større enn tallet 0,06, som igjen er ti ganger større enn 0,006. Hvis man legger sammen alle tallene i en kolonne, vil alle nuller skyves ut, og man får for eksempel 6666,666, der den siste sekseren er tallet i nederste rad. Dersom man hopper litt mellom kolonnene, kan man for eksempel konstruere tallet 6381,367, eller man kan klare seg med færre rader, og lage tall som 55,55 eller 45,36. Hele tiden går man én kolonne ned for hvert siffer, og da bruker man sifre som er tidelen av sifrene i raden over.

            Felles for alle rader, er at ingen tall inneholder flere enn ett siffer, bortsett fra plassholderen 0. Når man er ferdig med en rad, må man hoppe til begynnelsen på neste rad. Man har at ”ti niere = 90, ti tiere = 100, ti hundrer = 1000”, eller at ”ti tusendeler = en hundredel = 0,01, ti hundredeler = en tidel = 0,1 og at ti tideler = 1”.

Et alternativ kan være å skrive tallene slik:

Eller kanskje slik:

Poenget er å få fram størrelsesrelasjonene mellom radene i tabellen.

 

Misforståelser

Stevin forklarte desimalbrøksystemet på en utmerket måte. Dessverre er det altfor mange skoleelever som ikke forstår systemet like godt. Vi vet at det vrimler med misforståelser i skolen når det gjelder desimaltall. En medvirkende årsak er sannsynligvis at det blir arbeidet for lite med å se sammenhengen mellom desimalene, slik som forklart over.

            Den vanligste misforståelsen, eller uklarheten, er at elevene ser desimalene (sifrene bak kommaet) som et selvstendig tall, uavhengig av heltallsverdien. Derfor tror mange at for eksempel 7,45 er mer enn 7,5, fordi 45 > 5. Man kan finne et utall eksempler på dette, også blant lærerstudenter. Det finnes imidlertid også elever som tror at tallet blir mindre jo flere desimaler det har, noe som sannsynligvis skyldes en slags overgeneralisering av det man har fått høre om at desimalene blir stadig mindre jo flere det blir av dem. Slike misforståelser kan enkelt testes ved hjelp av enkle oppgaver, som å sortere tall etter størrelse, eller ved direkte sammenligning mellom to tall.

En annen måte å avsløre usikkerhet om desimaltallene på, er å spørre om hvilket siffer som står for eksempel hundredelsplassen i et tall med minst tre desimaler. Mange elever vil si at det er 3-eren som står på hundredelsplassen i 7,362, fordi man leser tallet ”sju komma tre hundre og sekstito.

Hvordan kan man så forebygge eller avskaffe slike misforståelser? Et viktig tiltak må være å arbeide grundig med sammenhengene som er omtalt over under innføringen av desimaltallene. En bra måte å støtte opp under forståelsen er å arbeide med måltall. Det har lenge vært vanligere å bruke penger (kroner og øre). Dette ser ut til å ha hatt en uheldig virkning. For det første blir det lite variasjon i antall sifre, slik at øvelsen i å bruke systemet blir dårlig, og for det andre kan det ha bidratt til å skape misforståelsen der sifrene før og etter kommaet sees uavhengig av hverandre.

Måleenheter gir mye større mulighet for fleksible oppgaver enn valuta. Oppgaver av typen

1,7 kg + 6 hg

1,65 m + 23 dm + 49 cm

4 kg + 6,27 hg + 245 g

2 l + 6 dl + 5 cl + 8 ml

I dette tilfellet bør man bruke vertikal oppstilling og fylle ut med nuller slik at alle tallene får like mange desimaler:

            1,7 kg = 1,7 kg

            6 hg    = 0,6 kg

            Sum:      2,3 kg

            1,65 m = 1,65 m

            23 dm  = 2,30 m

            49 cm  = 0,49 m

            Sum:      4,44 m

            4 kg     =  4,000 kg

            6,23 hg = 6,270 kg

            245 g    = 0,245 kg

            Sum:      10,515 kg

2 l        = 2,000 l

6 dl      = 0,600 l

5 cl      = 0,050 l

8 ml     = 0,008 l

Sum:      2,658 l

Det er viktig at slike oppgaver inneholder både tieroverganger og øvelser i å plassere sifrene på riktig plass. Øvelsene kan godt kombineres med ulike former for praktisk trening med måleinstrumenter, men man må huske på at slike øvelser kun gir et erfaringsgrunnlag, og at matematikken kommer etterpå.

Desimaltall i multiplikasjon og divisjon

Under innføring av multiplikasjon som regneart, defineres multiplikasjon som gjentatt addisjon. Når vi multipliserer to tall, kan vi tolke det ene som multiplikand og det andre som multiplikator. Strengt tatt spiller det ingen rolle i hvilken rekkefølge vi skriver dette, men i norsk skole har det lenge vært vanlig å skrive multiplikator først. (I min skoletid gjorde man det motsatt.) Da får vi at

            5 × 3 = 3 + 3 + 3 + 3 + 3

Hvis multiplikanden er et desimaltall, er det fortsatt enkelt å bruke denne definisjonen:

            5 × 3,4 = 3,4 + 3,4 + 3,4 + 3,4 + 3,4

Men hva hvis den første faktoren er et desimaltall? Da bryter definisjonen sammen.

            5,2 × 3 = ? Hvordan skal vi ta 3 fem komma to ganger?

Og enda verre, hva hvis begge faktorene er desimaltall?

            5,2 × 3,4 =

Her bryter definisjonen av multiplikasjon som gjentatt addisjon.

De praktiske situasjonene der man få bruk for å multiplisere to desimaltall med hverandre, er når man har med måltall å gjøre. Ett eksempel er beregning av arealer. Vi skal for eksempel finne arealet av et rektangel med lengde 5,2 m og bredde 3,4 m. Andre eksempler er situasjoner med sammensatte enheter, slik som tid, fart og vei, eller energiforbruk:

Tilbakelagt strekning = 5,2 m/s × 3,4 s = 17,28 m

Strømforbruket = 5,2 kWh × 3,4 h = 17,28 kW

Å forstå slike oppsett krever god innsikt både i praktiske situasjoner og i regningsartene, og i sammenhengen mellom dem. Et hovedpoeng er at man på et gitt tidspunkt må utvide definisjonen av multiplikasjon. Det samme gjelder divisjon, som vi i utgangspunktet kan definere som gjentatt subtraksjon (8 : 2 = antall ganger du må trekke 2 fra 8 for å få 0, dvs. 4 ganger.)

Multiplikasjon og divisjon anvendes på svært mange områder innen matematikken. Vi kan for eksempel multiplisere vektorer, matriser eller tensorer. Addisjon og subtraksjon kan bare brukes på et nokså begrenset antall situasjoner, mens multiplikasjon og divisjon kan brukes på et ubegrenset antall situasjoner, også på et vell av praktiske problemer. På tross

av kompleksiteten kan man likevel lage en klassifisering over praktiske situasjoner[1].

 

Oppsettet over er ikke entydig. Enkelte situasjoner kan oppfattes på ulike måter og derfor innpasses på mer enn ett sted i skjemaet. Mange av disse situasjonene er intellektuelt krevende å forstå. Situasjoner med avledede størrelser er vanskeligst, dvs. størrelser med mål som kilometer per time, meter per sekund eller gram per kubikkcentimeter (tetthet). Én forutsetning for å forstå dette er evnen til å reversere, slik at man kan turnere uttrykk som S = v × t, M = V × d fram og tilbake. Den beste forberedelsen for dette er på et tidlig tidspunkt å jobbe med slike sammenhenger som at når 9 × 7 = 63, så er 63 : 9 = 7 og 63 : 7 = 9.

Misforståelser i multiplikasjon og divisjon

En av de aller vanligste misforståelsene i grunnskolematematikken er å tro at man alltid får mer hvis man ganger og mindre når man deler. En av grunnene til at det blir slik, er at det blir arbeidet for lite med praktiske situasjoner der desimaltall inngår. Skal man arbeide med slike situasjoner, må man imidlertid utvide multiplikasjonsbegrepet, slik som omtalt i matrisen over. Det nytter ikke lenger å bare se på multiplikasjon som gjentatt addisjon.

            Det vrimler av eksempler på hvordan elever gjør feil med desimaltall. Et godt eksempel kan være dette:

• Epler koster 19,80 kr per kg. Hvor mye må du betale for 3,5 kg?
• Epler koster 19,80 kr per kg. Hvor mye må du betale for 0,65 kg?

Et stort antall elever multipliserer i det første tilfellet, men dividerer i det andre.

• 1,2 kg fisk koster 43,20 kr. Hva er prisen per kg?
• 0,8 kg fisker 28,80 kr. Hva er prisen per kg?

Her er det motsatt. Elevene dividerer i det første tilfellet, men multipliserer i det andre.

En annen måte å teste elevenes innsikt i oppgaver med desimaltall, er å be dem lage tekster som passer til ferdige oppstillinger. Lag en tekst som passer til oppstillingen:

• 4 × 7 = 28
• 28 : 7 = 4
• 0,4 × 0,7 = 0,28
• 0,28 : 0,4 = 0,7

Elever kan enkelt lage tekster til de to første variantene, men møter uoverstigelige problemer når de skal lage tekster som passer til de to siste.

Mer om multiplikasjon

Dersom den ene faktoren i et produkt ligger mellom 0 og 1, vil resultatet bli mindre enn den største faktoren:

               

Dersom begge faktorene ligger mellom 0 og 1, vil resultatet være mindre enn hver av de to faktorene:

           

For å få elever i grunnskolen til å forstå dette, bør man bruke praktiske situasjoner som grunnlag for læringen:

• Vi har 2 plankestykker som hver av dem er 0,4 m lange. Hvor lange er de til sammen?
• Hvor mange liter saft kan du helle i 2 glass som hver av dem tar 0,4 liter?
• Du går i 2 timer med en fart på 0,4 mil per time. Hvor langt går du?
• Et rektangel er 2 m langt og 0,4 m bredt. Finn arealet.
• Tettheten for et svært lett type treverk er 0,4. Hvor mye veier 2 dm³ av treverket?

Alle disse oppgavene fører til oppstillingen . De fleste elever vil intuitivt forstå at resultatene her vil bli mindre enn 2, i hvert fall i de tre første eksemplene. De to siste er mer krevende, men hvis elevene har forstått arealbegrepet og måleenhetene for areal, og fått tak i tetthetsbegrepet, vil svarene føles naturlige.

• Et rektangel er 0,2 m bredt og 0,4 m langt. Finn arealet.
• Du har et tøystykke som er 0,2 meter langt og klipper vekk 40 % av lengden. Hvor lang er biten som du klipper vekk?
• 2/10 av elevene ved en skole går i 7. klasse. 4/10 av disse igjen er gutter. Hvor stor andel av elevene ved skolen er 7.-klassegutter?
• En dame spaserer med en fart på 0,2 km/h. Hun går i 0,4 timer (24 minutter). Hvor langt går hun?

I alle eksemplene over kan man lage oppstillingen . I det første og det siste eksempelet er dette opplagt. I eksempel 2 kan man, hvis man ønsker, gjøre om 40 % til 0,4. I eksempel 3 vil det være et kunstgrep å bruke desimaltall, men det er fullt mulig, om man så ønsker. Sammenhenger i matematikken er som sagt viktig, og man kan jo også vise noen slike sammenhenger ved hjelp av dette eksempelet. Jeg skal for øvrig vise flere slike sammenhenger lengre ned.

Mer om divisjon

Når finnes i prinsippet to typer divisjon: delingsdivisjon og målingsdivisjon. Den første varianten er den naturlige delingen i mindre mengder, der vi skal finne hvor mye det er i hver mengde. Hvis tre barn skal dele tolv drops likt mellom seg, vil de få fire hver. Dette er en enkel situasjon som de fleste barn forstår intuitivt. Verre er det med målingsdivisjon, der man skal finne antall delmengder, ikke størrelsen av hver enkelt. Man dividerer da i de fleste situasjoner med et måltall (benevnt tall). Rent formelt kan man definere delings- og målingsdivisjon slik:

Produkt: multiplikator · multiplikand = produkt

Delingsdivisjon: Produkt : multiplikator = multiplikand

Målingsdivisjon: Produkt : multiplikand = multiplikator

Det er tvilsomt om denne definisjonen er særlig klargjørende, og når man opererer med sammensatte enheter, eller når man regner arealer, blir skillet mellom delings- og målingsdivisjonen opphevet, men det kan jo være greit for lærere å kjenne den.

Et eksempel på delingsdivisjon:

Fem personer skal dele en gevinst på 100 000 kr likt mellom seg.
Hver person får:

Tilsvarende målingsdivisjon:

Noen personer skal dele en gevinst på 100 000 kr likt mellom seg.

Et annet eksempel på delingsdivisjon og tilsvarende målingsdivisjon:

En 4 m lang planke deles 8 biter, hver av dem på 0,5 m (= ½ m)

Delingsdivisjon:

Lengden av hver bit = 4 m : 8 = 0,5 m

Målingsdivisjon:

Antall biter: 4 m : 0,5 m = 8               (4 m : ½ m = 8)

Poenget her er at divisjon med desimaltall nesten alltid er målingsdivisjon[1]. Men hvis man innser dette, vil også her resultatene stemme med intuisjonen. Problemstillingene som fører til divisjon med desimaltall er for øvrig nøyaktig de samme som fører til divisjon med brøk. Desimaltall er jo egentlig brøker (såkalt desimalbrøk), så dette er egentlig en selvfølge.

Har man først innsett at divisjon med desimaltall er målingsdivisjon, er det enkelt å masseprodusere oppgaver:

• Du har 1,5 liter brus som du heller i glass som tar 0,3 dl. Hvor mange glass kan du fylle?
• Blyanter koster 0,50 kr hver. Hvor mange blyanter får du for 10 kr?
• Arealet av et rektangel er 0,08 m². Bredden er 0, 2 m. Finn lengden.
• Et trestykke veier 7,2 kg. Tresorten har tetthet 0,9 (kg/dm³). Finn volumet av trestykket.
• Prisen for elektrisitet er å et tidspunkt 0,75 kr/kWh. Hvor mange kilowattimer kan du bruke for 3000 kr?

Med litt trening bør det være overkommelig å innse at i alle tilfellene over, må man dele med et desimaltall (hvis man ikke unngår problemet ved å gjøre om måleenhetene). Vi ser imidlertid at mange skoleelever gjør feil på dette, selv om de har tekstene foran seg. Flertallet av disse innser sannsynligvis intuitivt at svarene er større en dividenden, men når de samtidig tror at du må gange for å få mer, så multipliserer de i stedet for å dividere. Når de så kommer ut med et urimelig svar, fikser de på resultatet ved å sette kommaet på feil sted, slik at svaret ser noenlunde rimelig ut.

Nødvendigheten av å analysere tekster

Erfaringer og forskning viser at elever ofte leser tekstene i oppgavene svært overfladisk, eller nærmest hopper helt bukk over dem. De bruker i stedet selvlagede strategier som stemmer overens med deres egne erfaringer og, svært ofte ufullstendige, oppfatninger. Én slik strategi er å se på tallene, ut fra den formening at tallene i seg selv forteller hvilken regneoperasjon man skal bruke. Er tallene 25 og 30, eller 25 og 0,5, er sjansen stor for at man skal gange. Er tallene 3000 og 25, er det mest sannsynlig at man skal dele. Denne strategien kombineres md å vurdere om svaret er noenlunde rimelig. Hvis ikke prøver man en annen regningsart, eller man fikser på svaret ved å manipulere med kommaet.

En annen hyppig brukt strategi er å se etter nøkkelord i teksten. Ofte kan dette være en vellykket strategi, men ikke alltid. Midt på 1990-tallet ble det gitt en eksamensoppgave i ungdomsskolen som lød omtrent som følger:

Blyanter koster 0,20 kr per stykk. Hvor mange blyanter kan du få for 100 kr?

Svært mange elever multipliserte 0,20 med 100 kr og fikk 20 blyanter til svar. Her er det en kombinasjon av rekkefølgen av opplysningene og verdien av tallene som forleder elevene som ikke tenker seg om, til å velge feil algoritme. Man kunne ikke forvente annet enn at mange elever skulle bomme på denne oppgaven, og det er for så vidt greit nok. Mye verre var det at mange sensorer protesterte på oppgaven og mente at opplysningene i oppgaven burde vært gitt i motsatt rekkefølge. Disse sensorene mente tydeligvis at oppgaver i matematikk bør lages slik at elever kan få bruke slike overflatiske strategier som omtalt over, i stedet for å måtte tenke gjennom oppgaveteksten. Men dette er jo stikk i strid med vår kunnskap om effektiv læring. Det er nettopp selvstendig tenkning som utvikler de matematiske ferdighetene.

            Skolen må påta seg deler av skylden for at elevene tar i bruk uholdbare snarveier når de skal løse tekstoppgaver. Det er viktigere å bruke tid på å analysere og diskutere tekstene enn det er å masseprodusere svar.

Noen matematiske sammenhenger

Som nevnt mange andre steder, er det alltid nyttig og interessant å se på sammenhenger i matematikken. Dersom vi beregner arealer, kan vi for eksempel studere sammenhengen mellom måleenhetene, og sammenhengen mellom disse og desimaltallene.

            5,2 cm × 3,4 cm = 52 mm × 34 mm

Vi får her benevnelsen mm². Etter vi har utført beregningen, kan vi godt gjøre om svaret til cm², ved å sette komma slik at vi får to desimaler.

           

Dette kan jo være én måte å illustrere at det er en faktor på hundre mellom cm² og mm², samtidig som man ser sammenhengen mellom desimaltall og brøk, og hvordan man multipliserer brøker.

            I ungdomsskolen eller sent på barneskolen, kan det være aktuelt å vise en annen type sammenheng:

           

Dette har stor relevans for videre arbeid med algebra. Det er også mulig å se sammenhengen mellom den siste oppstillingen og nye algoritmer for multiplikasjon.         

Det kan være at det er å gå vel langt å vise elever alle disse sammenhengene, men lærere bør kjenne dem, og noen av de flinkeste elevene vil sikkert ha utbytte av det.

---

[1] Unntaket er slike tilfelle som dette: 3/4 av bøkene i et bibliotek er skjønnlitteratur. 1/5 av disse bøkene er skrevet av norske forfattere. Dvs. at 3/4 × 1/5 = 3/20 av bøkene er norsk skjønnlitteratur.

Omvendt: Hvis vi vet at 3/20 av bøkene er norsk skjønnlitteratur og at 3/4 av alle bøkene er skjønnlitteratur, kan vi finne andelen av skjønnlitteraturen som er norsk ved å ta 3/20 : 3/4 = 0,15 : 0,75. Det er vanskelig, eller i det minste svært kunstig, å bruke 3/4-delene som et måltall.

---

[1] Geer, B. (1992). Multiplication and division as models of situations. In Grouves. D.(Ed.), Handbook of research in mathematics teaching and learning, 276 – 295. Macmillan, New York.

---

[1] Al-Khwarizmi har vært opphav til flere ting. Ordet algebra er en forvrengning av hans navn, og ordet algebra en forvrengning av en del av tittelen i hans mest kjente bok, Al-Kitāb al-mukhtaṣar fī hīsāb wa’l-muqāba, en bok om ligninger. Ordet al-ğabr handler om å legge til like mye på begge sider av en ligning, slik at man flytter negative ledd over på motsatt side av likhetstegnet.

[2] Clavius er mest kjent som personen bak Den gregorianske kalenderen.

[3] Napier er kjent for å ha funnet opp logaritmene.