På slutten av 60-tallet introduserte Egil Wiken for norsk skole en ny måte å føre svar på tekstoppgaver på. Dette var systemet med såkalte svarsetninger. Hensikten var å frita elevene for bryderiet med å lage nitidige tekster til alle oppstillinger og tall. Wiken mente at dette kunne frigjøre tankene fra unødvendig formalisme og gi elevene rom til heller å tenke på selve oppgaveløsningene.
Wikens hensikt med nyordningen var nok god, men etter min mening er den noe av det aller mest uheldige som er gjort innen matematikkundervisningen her til lands. I stedet for å frigjøre elevene fra formalisme, førte det til at løsning av tekstoppgavene ble en slags tallmagi, der strukturen i løsningene kom i bakgrunnen. Vi vet i dag at svært mange elever har en tilbøyelighet til å gjette på løsninger ut fra tallenes beskaffenhet, i stedet for å tenke gjennom hele problemstillingen. La meg ta et par eksempler:
Oppgave: 100 biter smågodt koster 50 kr. Hvor mye koster 1 bit?
Her vil mange elever dele 100 med 50 og få 2 kr til svar. Når de ser at det spørres etter prisen på 1 bit, assosierer de med deling, men faller i den fellen, eller vanen, at de deler det største tallet med det minste, eller det første tallet i teksten med det andre.
Oppgave a: 1 kg fisk koster 89,50 kr. Hvor mye koster 1,6 kg ?
Oppgave b: 1 kg fisk koster 89,50 kr. Hvor mye koster 0,75 kg ?
Veldig mange elever begynner å dele tallene i oppgave 2 med hverandre, selv om de først regner riktig på den første oppgaven. Sannsynligvis henger dette sammen med en forstilling om at man alltid får mindre når man deler, og det er jo riktig at man skal få mindre enn 89,50 kr.
Dersom man skal motarbeide slike tilbøyeligheter, må man arbeide med strukturene i problemet, dvs. slike sammenhenger som at:
- Pris per enhet er lik samlet pris dividert med antall enheter
- Samlet pris er lik pris per enhet ganget med antall enheter
- Antall kjøpte enheter kan beregnes ved å dividere samlet pris med prisen per enhet
Slike sammenhenger må synliggjøres, diskuteres og eksemplifiseres gjentatte ganger, og det må vises at strukturene gjelder uavhengig av tallenes størrelse. For å få system i dette er bruk av tekster et nødvendig redskap.
Et annet sentralt argument for bruk av gammeldags teksting, er at den som ser løsningen skal forstå hva som er gjort, uten at vedkommende skal behøve å ha oppgaveteksten foran seg. Det er umulig når man bruker svarsetninger. Et oppgavesvar skal være noe mer enn bare å gi et riktig svar. Et like viktig mål er å presentere en løsning slik at tankegangen i løsningen er synlig for leseren. Bruk av svarsetninger bidrar bare til å opprettholde den svært uheldige svarfikseringen som vi ser altfor mye av matematikkfaget i skolen. Det må imidlertid være mulig å eksperimentere og prøve seg fram på kladd, men dette skal alltid føre fram til en ordentlig presentasjon av løsningen på en slik måte at føringen forteller om tankegang og regnemetode.
Å bruke teksting slik som beskrevet under, er en selvfølge i andre sammenhenger. Tenk bare på nyheter i avisene. De kan ikke bare skrive ned en masse tall uten forklaring, for så å skrive en konklusjon til slutt. Eller tenk å et kommunebudsjett. Ingen tall presenteres uten at det står forklart hva det dreier seg om.
Regler for føring
Hovedregelen er meget enkel:
- Presenter aldri et tall eller en størrelse uten at du først skriver hva det dreier seg om.
Dersom vi for å kunne presentere en verdi, må ha en utregning først, gir vi en oppstilling som viser hvordan vi finner fram til denne verdien. Selve utregningen behøver vi derimot ikke vise. Det kan vi gjøre på kladd, eller vedhjelp av et elektronisk hjelpemiddel.
Ut fra dette vil en typisk føring se slik ut:
- Tekst: oppstilling = ønsket verdi
Vi får for eksempel vite at 85 % av massen i en metallgjenstand er sølv. La oss si at gjenstanden har en masse på 400 gram , og du skal finne sølvmengden. Da bør du føre slik:
Tekst og oppstilling kan selvsagt utformes på flere måter. Hensikten er å vise hva du er ute etter å finne og hvordan du finner det. Vi kan for eksempel skrive  eller
eller  . For en skoleelev kan det være vanskelig å skrive en god tekst, men som oftest kan man bare skrive om spørsmålet i oppgaveteksten.
. For en skoleelev kan det være vanskelig å skrive en god tekst, men som oftest kan man bare skrive om spørsmålet i oppgaveteksten.
 eller
eller  . For en skoleelev kan det være vanskelig å skrive en god tekst, men som oftest kan man bare skrive om spørsmålet i oppgaveteksten.
. For en skoleelev kan det være vanskelig å skrive en god tekst, men som oftest kan man bare skrive om spørsmålet i oppgaveteksten. Som oftest er det nødvendig med to eller flere regneoperasjoner, og da kan det være naturlig eller nødvendig å bruke flere linjer:
Ordinær pris: 6000 kr
Vi må betale: 5700 kr
Før i tiden var det viktig at man markerte svaret ved å sette to streker under det. I eksemplene over har jeg gjort det. Dersom man måtte foreta mellomregninger, dvs. finne størrelser som ble brukt videre for å finne det endelige svaret, skulle man sette én strek under dette resultatet. I dag virker imidlertid dette noe kunstig, spesielt sett i lys av at man ofte vil presentere ting elektronisk. Da kan det være mer hensiktsmessig å markere svaret på annen måte, for eksempel ved hjelp av en utheving, eller ved hjelp av farger. Det kan for eksempel se slik ut i et regneark:
Ordinær pris: | 6000 | kr | |
Rabatt: | 6000 kr * 5 % = | 300 | kr |
Vi må betale | 5700 | kr | |
I noen sammenhenger kan man sette sammen de to beregningene i én oppstilling:
Det bør da gå klart fram av sammenhengen hva som foregår. Jeg vil nok anbefale at man stort sett venter til ungdomsskolen med å bruke slike sammensatte oppstillinger.
En feil man ofte ser utrente elever gjøre, er å skrive tekst bare foran tallet i den første linjen, og da brukes gjerne teksten som hører hjemme i tredje linje. Dette er trolig et resultat av at elevene har vært vant til å bruke svarsetninger og derfor mangler trening i å føre skikkelig. Jeg har diskutert problemene rundt føring med mange barneskolelærere. Omtrent alle har sagt at kravet om føring med tekster, slik som vist over, for dem gjerne kan innføres i ungdomsskolen, men at det ikke passer i barneskolen. Jeg er ikke enig i dette. Erfaringen viser at elever som har vent seg til systemet med svarsetninger, har etablert vaner som det er svært vanskelig å endre. ”Vond vane er vond å vende” sier et gammelt visdomsord. Ordene gir en god beskrivelse av de problemene man møter når man prøver å avvenne elever med å bruke disse uhensiktsmessige svarsetningene.
Føring av måleenheter
Så lenge vi opererer med bare én enkelt måleenhet, slik som i eksemplene over, er dette uproblematisk. Verre blir det når vi har sammensatte størrelser. Hvordan håndterer vi for eksempel areal- og volumenheter? Skal vi skrive
eller
Jeg vil i utgangspunktet anbefale den første skrivemåten i barneskolen, men vil ikke være bastant. Det kan være vanskelig for en barneskoleelev å forstå at  . På den annen side gir nettopp denne skrivemåten en god anledning til å diskutere hva måleenhetene kvadrat- og kubikkmeter egentlig er for noe, og slike diskusjoner kan man aldri få for mange av. En slik diskusjon kan imidlertid like gjerne føre til at man velger den første føringsmetoden.
. På den annen side gir nettopp denne skrivemåten en god anledning til å diskutere hva måleenhetene kvadrat- og kubikkmeter egentlig er for noe, og slike diskusjoner kan man aldri få for mange av. En slik diskusjon kan imidlertid like gjerne føre til at man velger den første føringsmetoden.
 . På den annen side gir nettopp denne skrivemåten en god anledning til å diskutere hva måleenhetene kvadrat- og kubikkmeter egentlig er for noe, og slike diskusjoner kan man aldri få for mange av. En slik diskusjon kan imidlertid like gjerne føre til at man velger den første føringsmetoden.
. På den annen side gir nettopp denne skrivemåten en god anledning til å diskutere hva måleenhetene kvadrat- og kubikkmeter egentlig er for noe, og slike diskusjoner kan man aldri få for mange av. En slik diskusjon kan imidlertid like gjerne føre til at man velger den første føringsmetoden.Dersom man kommer fram til at enighet om at én rute har arealet  , er det naturlig å bruke den første oppstillingen.
, er det naturlig å bruke den første oppstillingen.
 , er det naturlig å bruke den første oppstillingen.
, er det naturlig å bruke den første oppstillingen.På bakgrunn av det siste argumentet, heller jeg til at man bør bruke den første oppstillingen i barneskolen. I ungdomsskolen kan imidlertid dette endre seg, for der kommer elevene oftere i kontakt med andre sammensatte enheter, slik som enheter for hastighet, tetthet eller energi.
Innen naturvitenskapene regner man med måleenhetene akkurat som man gjør med tall. Det er egentlig det jeg også har gjort i eksemplene over. Dersom beregningene er kompliserte eller uoversiktlige, kan det å regne på måleenhetene være et godt redskap for å sjekke om man gjør ting riktig. Som oftest vet man hvilken måleenhet man skal få til slutt. Derfor kan en slik analyse gi en god indikasjon på om man bruker riktig beregningsmåte. En slik analyse kalles dimensjonsanalyse. Jeg gir et enkelt eksempel på det i kapitlet om analyse av en tekstoppgave.
Misbruk av likhetstegnet
I matematikken har likhetstegnet en absolutt betydning, dvs. at uttrykk som står på hver sin side av et likhetstegn skal være like eller likverdige. Det er ikke slik alle steder. I dataprogrammer brukes likhetstent gjerne som et signal om at en bestemt handling skal utføres. Svært mange skoleelever har en intuitiv oppfatning av likhetstegnet som er i tråd med en slik tolkning. ”Når vi har utført en beregning, kan vi skrive likhetstegn for å vise at vi regner videre”, eller en lignende tankegang. Et typisk eksempel på dette er at man sløyfer måleenheter i oppstillinger og skriver dem bare i svaret. Et tydeligere eksempel på mangelfull oppfatning av likhetstegnets betydning, ser man ofte i forbindelse med regning med fortegnstall. Vi kan for eksempel se slik føring som dette:

Denne føringen er høyst ukorrekt, for her misbrukes likhetstegnet to ganger. En korrekt føring vil se slik ut:
Man kan selvsagt også regne i en annen rekkefølge, for eksempel slik:
Uansett hvordan man regner, må man passe på å ikke sløyfe noen av verdiene under veis. I litt mer avansert matematikk, der beregningene blir lengre og mer kompliserte, er dette særs viktig. Elever bør derfor vennes til å bruke likhetstegnet korrekt så tidlig som mulig. Man må være oppmerksom på at dette ikke kommer av seg selv.
Ukorrekt bruk av likhetstegnet er bare ett av mange eksempler på at intuisjonen kan lede elever på feilspor. Forekomsten av slike misforståelser er uunngåelige og forekommer svært hyppig. Diskusjoner og klargjøring av hva som er matematisk korrekt, er og blir noe av det viktigste en matematikklærer kan bidra til.






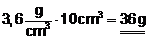



Ingen kommentarer:
Legg inn en kommentar